新英雄即将进驻
各位朋友大家好我是解说家,本周锤子活动已经进入最后倒计时,即将迎来新一期英雄的进驻,那么本周5的英雄又能带来多少惊喜呢?
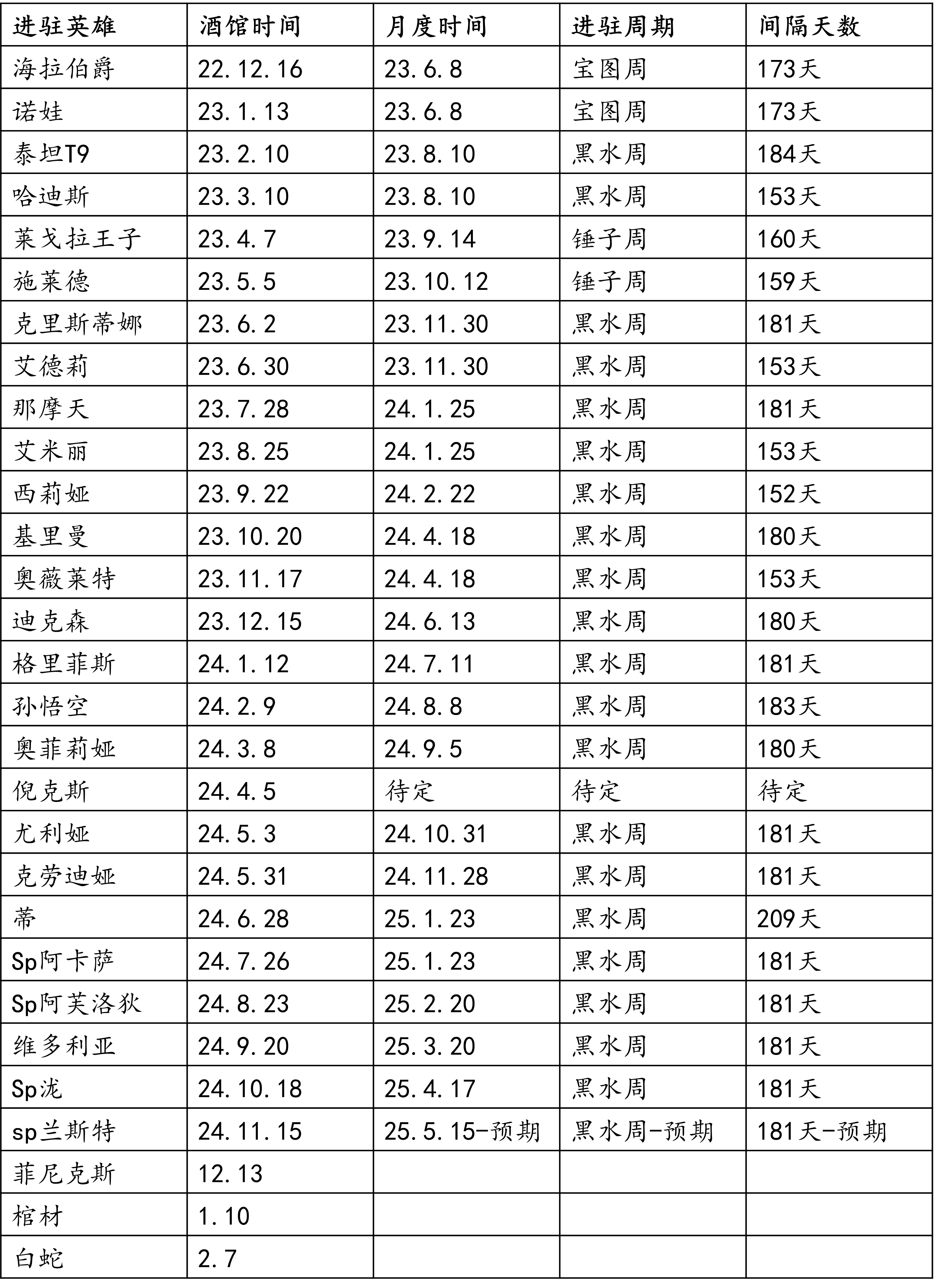
本期新英雄情况
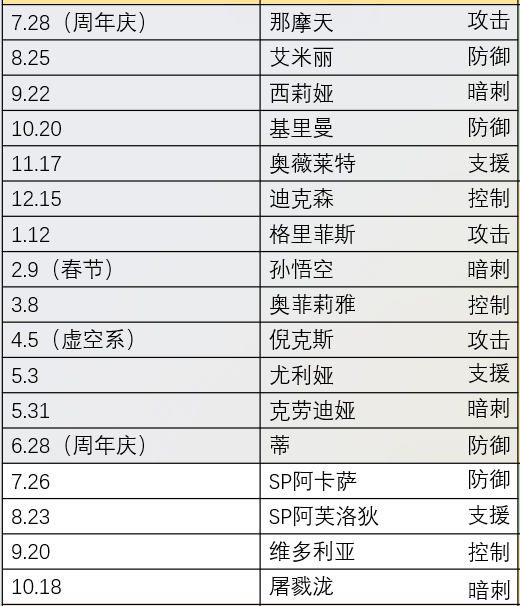
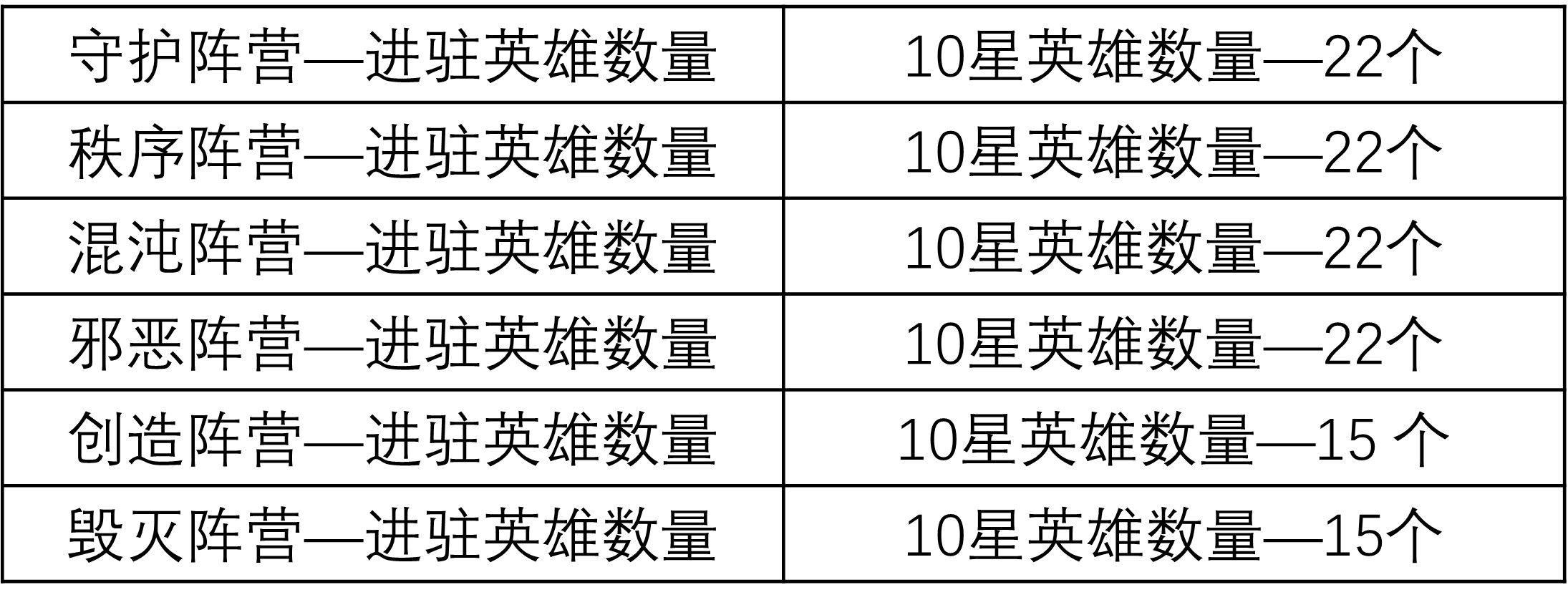
通过进驻情况可以看出,上一阶段4系以守护阵营克劳迪娅收尾,本阶段4系以邪恶阵营sp阿卡萨开头,混沌屠戮泷收尾,从进驻情况可以看出4系阵营已经全部出完,而创造毁灭阵营也随着维多利亚的补充也全部进驻完毕,那么新一期英雄的进驻只能是重新以4系开始循环,要么轮到新增的虚空系来补位
遣散商店更新
本期除邀请得好礼外,还值得部分玩家关注的点就是英雄归来(英雄归来=遣散币商店换购英雄),那么本期的英雄归来会带来哪两位英雄进驻呢?
|
10000 |
瑰月(7月) 9000 |
|
13000 |
阿努比斯(8月) 9000 |
|
9500 |
丝西娜(9月) 7500 |
|
13000 |
艾莉瑞尔(10月) 9000 |
|
10000 |
王(11月) 8500 |
|
12000 |
奥黛丽夫人(12月) 8500 |
|
那摩天(狼人可乐) 12000 |
索菲亚(1月) 9000 |
|
9000 |
艾莉瑞尔(2月) 7500 |
|
13000 |
诺娃(3月) 8000 |
|
10000 |
丝西娜(4月) 7500 |
|
13000 |
阿努比斯(5月) 8000 |
|
12000 |
蕾贝卡(5.31) 8000 |
|
10000 |
艾莉瑞尔(6.28) 7500 |
|
倪克斯(梦魇卡萨) 13000 |
艾德莉(7.26) 8000 |
|
孙悟空(龙袭阿芙) 12000 |
拉王子(8.23) 8000 |
|
格里菲斯(维多利亚) 10000 |
艾丽米(9.20) 7500 |
|
蒂(屠戮泷) 13000 |
诺娃(10.18) 8000 |
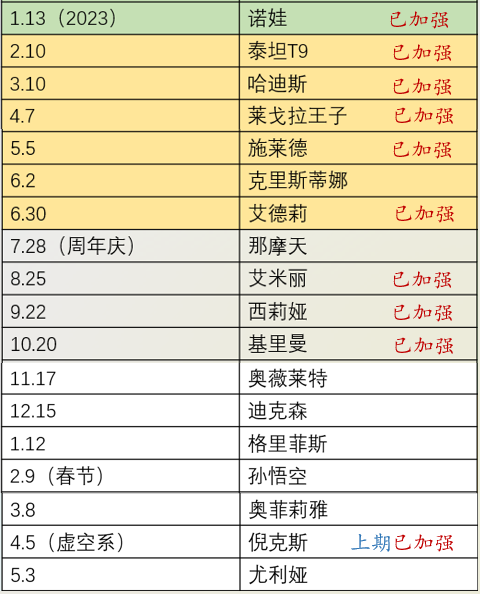
上期10月份可乐英雄屠戮泷进驻,同时迎来蒂延期一个月时间进驻遣散币商店,按照惯例本期正常该回归到4系阵营的二线英雄进驻,按照时间该轮到西莉娅/迪克森的进驻,但这两个英雄作为主英雄属实都有些太过寒酸,所以不排除继续用基里曼来充数的可能
通过分析得出:本期商店返厂英雄期待值都不是太高,缺月币的半新区玩家对基里曼有需求的可以做提前计划(预计需要1300遣散币,遣散币遣散优先级:依次为,3星>5星>4星(3星(10遣散币)、5星(250遣散币)、4星(25遣散币)、6星/7星/8星(1250遣散币)
好了, 以上就是本期的全部内容~~







发表评论 取消回复